Le master Mathématiques Appliquées, Statistique (MAS) est une formation en deux ans : BAC+4, BAC +5.
Il a pour vocation de former des mathématiciens modélisateurs pouvant s’impliquer, au sortir de la formation, dans des secteurs d’activités variés. En effet, les mathématiques appliquées touchent de nombreux secteurs d’activités, aussi diversifiés que l’environnement, le marketing, l’industrie pharmaceutique, la santé publique, le contrôle qualité, la fiabilité, les enjeux bancaires, le marché des assurances, l’industrie automobile…, et ce, au sein des organismes de recherche ou des services R&D de grands groupes.
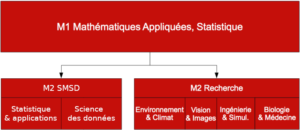
La formation consiste en une première année commune de M1 « Mathématiques appliquée, statistique » permettant d’acquérir des connaissances en mathématiques appliquées regroupant modélisation, techniques d’analyse théorique et numérique, probabilités, statistique ; le tout allié à une mise en oeuvre informatique et logicielle.
Deux spécialités sont proposées en seconde année :
- M2 orienté recherche académique & industrielle Maths en action : du concept à l’innovation
- M2 orienté ingénierie mathématique M2 Statistique, modélisation et science des données (SMSD), ouvert à la formation initiale, continue et en alternance
Il accueille également deux spécialités de M2 intra-mentions : Compétence Complémentaire en Informatique (CCI) et Ingénierie technico-commerciale (ITC)
La première année de la formation (M1) ainsi que le parcours Maths en Action bénéficient depuis le printemps 2019 d’une labellisation de la part de l’IDEX Lyon.
Contacts
Scolarité du département de Mathématiques : Scolarite.Mathematiques@univ-lyon1.fr
Simon MASNOU masnou@math.univ-lyon1.fr +33 (0)4 72 43 13 86
M1 > Christophe POQUET poquet@math.univ-lyon1.fr +33 (0)4 72 44 79 39
M2 Maths en action > Simon MASNOU masnou@math.univ-lyon1.fr +33 (0)4 72 43 13 86
M2 SMSD > Gabriela CIUPERCA Gabriela.Ciuperca@univ-lyon1.fr +33 (0)4 26 23 45 57
Master MAS
Université Claude Bernard Lyon1
Scolarité Département de Mathématiques
Bâtiment Braconnier
21, avenue Claude Bernard
69622 VILLEURBANNE CEDEX
